The question was asked about how a tipload calculation could be done under stringing (initial) conditions.
AS/NZS 7000:2016 describes final conditions throughout, although initial conditions are referred to in some of the appendices.
Initial conditions is the state of the conductor when it is first installed. After installation, permanent (plastic) elongation occurs over the life of the line. This permanent elongation is called creep. After 10 years the line is considered to be in final conditions.
HB331:2020 describes a temperature offset method to estimate initial conditions from final conditions, stating that “conductor permanent elongation is equated to an equivalent conductor thermal elongation” (section 5.7.1).
Take this stringing table as an example (Iodine conductor @ 12% CBL):
| SPANS | 0 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| 70 | 0.46 | 0.51 | 0.57 | 0.63 | 0.68 | 0.74 | 0.79 | 0.84 | 0.89 | 0.94 | 0.99 |
| 80 | 0.6 | 0.67 | 0.74 | 0.82 | 0.89 | 0.96 | 1.03 | 1.1 | 1.17 | 1.23 | 1.29 |
| 90 | 0.76 | 0.85 | 0.94 | 1.04 | 1.13 | 1.22 | 1.31 | 1.4 | 1.48 | 1.56 | 1.64 |
| 100 | 0.94 | 1.05 | 1.16 | 1.28 | 1.39 | 1.51 | 1.62 | 1.72 | 1.83 | 1.93 | 2.02 |
| 110 | 1.14 | 1.27 | 1.41 | 1.55 | 1.69 | 1.82 | 1.96 | 2.09 | 2.21 | 2.33 | 2.45 |
| 120 | 1.35 | 1.51 | 1.67 | 1.85 | 2.01 | 2.17 | 2.33 | 2.48 | 2.63 | 2.78 | 2.92 |
and apply a 15° temperature offset to approximate Initial conditions, as recommended by HB331:
| SPANS | 0 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| 70 | 0.46 | 0.51 | 0.57 | 0.63 | 0.68 | 0.74 | 0.79 | 0.84 | |||
| 80 | 0.6 | 0.67 | 0.74 | 0.82 | 0.89 | 0.96 | 1.03 | 1.1 | |||
| 90 | 0.76 | 0.85 | 0.94 | 1.04 | 1.13 | 1.22 | 1.31 | 1.4 | |||
| 100 | 0.94 | 1.05 | 1.16 | 1.28 | 1.39 | 1.51 | 1.62 | 1.72 | |||
| 110 | 1.14 | 1.27 | 1.41 | 1.55 | 1.69 | 1.82 | 1.96 | 2.09 | |||
| 120 | 1.35 | 1.51 | 1.67 | 1.85 | 2.01 | 2.17 | 2.33 | 2.48 |
Comparing the sags in the initial table to the corresponding values in the final table you see that the former is 30-35% smaller than the latter at typical stringing temperatures. Tension is inversely proportional to sag1 therefore initial tensions are of the order of 30% higher than final.
Considering that the tipload under maximum wind loading may be two to five times greater than the everyday loading, assuming you have designed the pole to support the wind load, this estimated 30% is not really significant.
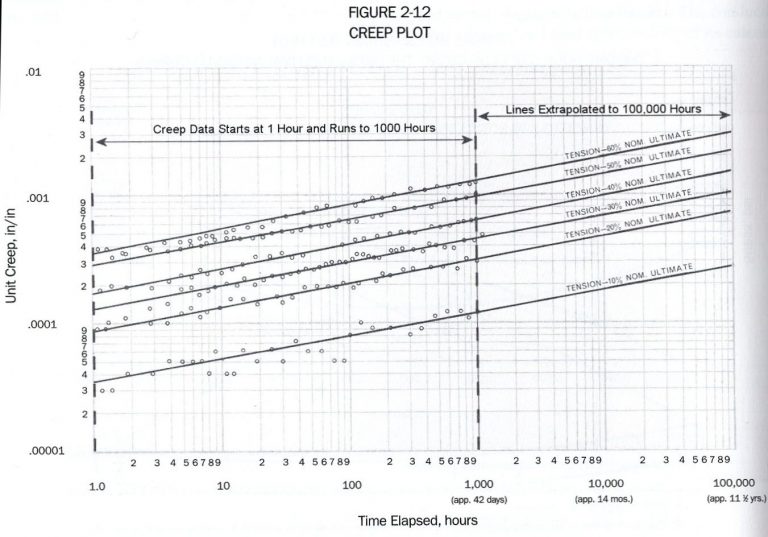
Another consideration is the fact that the initial conditions do not last very long. Southwire’s Overhead Conductor Manual has this chart of creep against time.
Deprecated: preg_replace(): Passing null to parameter #3 ($subject) of type array|string is deprecated in /users/ipowerma/public_html/wp-includes/kses.php on line 1744
This figure and the accompanying equations lead to the observation that
"for any period of time, when conductor tension and temperature are held constant, 70% of the creep occurs in the first 10% of the period." (2.5.3)
Do you need to evaluate the tipload for initial conditions? Probably not. But if you do want to, you could use the temperature-offset tensions for the calculation.
Deprecated: preg_replace(): Passing null to parameter #3 ($subject) of type array|string is deprecated in /users/ipowerma/public_html/wp-includes/kses.php on line 1744
